3.3 Erklärungsmodell Chaostheorie

Haken formuliert, dass die Chaostheorie als eine Untermenge der Synergetik verstanden werden kann. (Hak91, S. 58) Da sich die Chaostheorie jedoch relativ unabhängig von der Synergetik entwickelt hat, erfolgt hier ein kurzer Überblick. Auf eine mathematische Darstellung wird verzichtet und stattdessen eine topologische Darstellung (nach Flä98, S. 127ff) gewählt.

Der Begriff Chaos mag irreführend sein, da es sich nicht um die Bedeutung von Chaos im allgemeinen Sprachgebrauch handelt. Die Chaostheorie betrachtet kein völlig zufälliges Verhalten, wie z. B. die Brownsche Bewegung⁷. Um diesen Unterschied hervorzuheben, sprechen manche Autoren von deterministischem Chaos⁸.

Ausgangspunkt der Chaostheorie waren Untersuchungen durch den Meteorologen Lorenz in der 60er Jahren. Er versuchte die Wetterentwicklung mit einem Gleichungssystem vorherzusagen, welches lediglich auf drei Variablen (Temperatur, Luftdruck und Windrichtung) und drei Gleichungen basiert. Dieser Versuch scheiterte, da schon kleine Messfehler bei der Erhebung der aktuellen Wetterdaten zu sehr unterschiedlichen Vorhersagen führten. Obwohl eine mathematische Gleichung zugrunde lag, entwickelten sich die Ergebnisse unvorhersagbar. In diesem Zusammenhang wurde der Begriff deterministisches Chaos gebildet. Von Lorenz stammt das Sinnbild, wonach ein Schmetterlingsschlag⁹einen Sturm irgendwo anders auf der Welt auslösen kann.

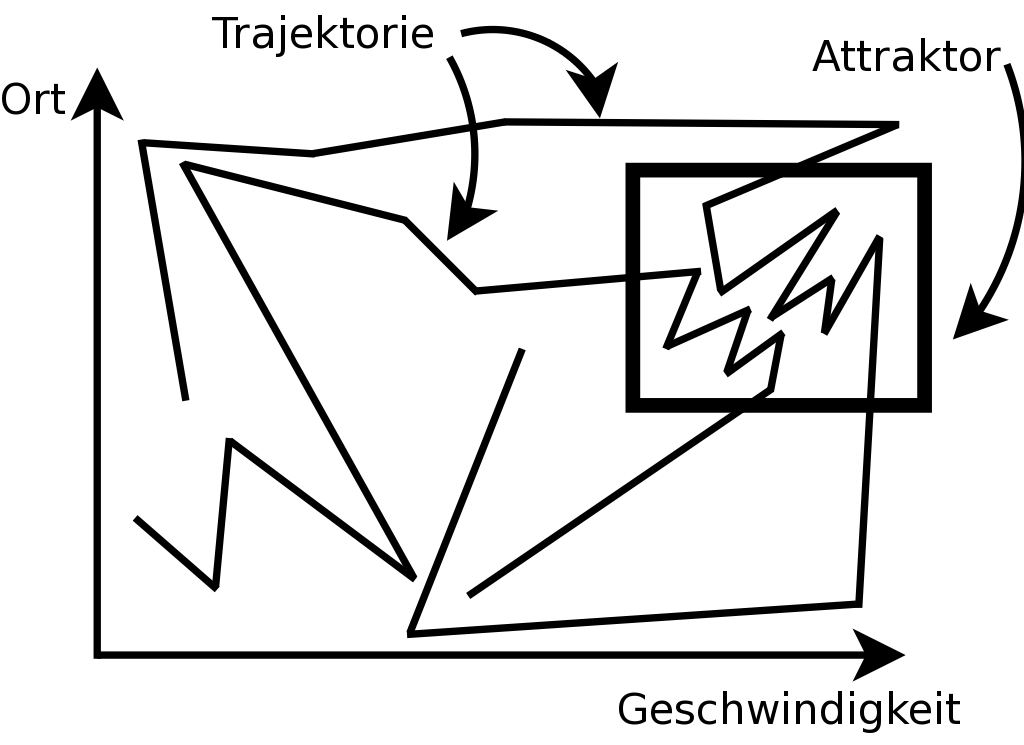
Der Zustand eines Systems bildet in einem beliebig dimensionalen Raum, bezeichnet als Phasenraum, einen Punkt. Der Phasenraum kann z. B. durch die Dimensionen Ort, Zeit und Geschwindigkeit gekennzeichnet werden. Zwischen den verschiedenen Zustandspunkten im Phasenraum ergibt sich eine Kurve. Diese Kurve wird als Trajektorie bezeichnet. Streben nun alle Trajektorien eines Systems, ausgehend von verschiedenen Startpunkten, auf einen bestimmten Bereich im Phasenraum asymptotisch zu, wird dieser Bereich als Attraktor bezeichnet. Der Attraktor bildet im Phasenraum einen Bereich, in dem sich das System relativ stabil verhält. Es ergibt sich das in Abbildung 3 auf Seite dargestellte Diagramm. Interessant ist weiterhin, dass der Bereich des Attraktors eine niedrigere Dimension als der Phasenraum besitzt und somit eine bessere Untersuchung des Systems möglich ist, da eine Vereinfachung vorliegt. Zum Verständnis soll erwähnt werden, dass im Rahmen der mathematischen Darstellung der Chaostheorie nicht ganzzahlige Dimensionen zulässig sind.

Abbildung 3: zweidimensionaler Phasenraum mit Trajektorien und Attraktor

In der Chaostheorie ist ein Attraktor von besonderem Interesse. Dieser wird als seltsamer Attraktor bezeichnet und zeigt einige spezielle Eigenschaften. Die sich dem seltsamen Attraktor asymptotisch nähernden Trajektorien erreichen jeden Punkt des seltsamen Attraktors ohne sich gegenseitig zu schneiden. Hier spricht man von Struktur. Auf der anderen Seite ist das Verhalten der Trajektorien völlig chaotisch, da die Trajektorien zwischen den einzelnen Punkten des seltsamen Attraktors ohne erkennbare Logik springen. Benachbarte Punkte liegen demnach auf unterschiedlichen Trajektorien und dadurch lässt sich begründen, warum kleinste Änderungen, Fluktuationen, zu sehr unterschiedlichen Ergebnissen führen.

Vom Phasenraum zu unterscheiden ist der Parameterraum. In diesem Raum wird das Verhalten verschiedener Systeme dargestellt. Die Systeme sind sich ähnlich, weichen lediglich durch die Werte der Parameter ab. Prinzipiell verlaufen die Kurven im Parameterraum kontinuierlich, allerdings kann es passieren, dass sich an einem Punkt das Verhalten des Systems grundlegend ändert und somit eine Änderung der Systemparameter stattfindet. Diese Punkte werden als Bifurkationspunkte bezeichnet.

Während der Verlauf im Phasenraum mittels der Trajektorien nachvollzogen werden kann, scheint der Verlauf im Parameterraum völlig willkürlich. Deshalb spricht man von deterministischem Chaos. Der Verlauf im Parameterraum kann als Emergenz betrachtet werden. Eine Vorhersage scheint prinzipiell nicht möglich.

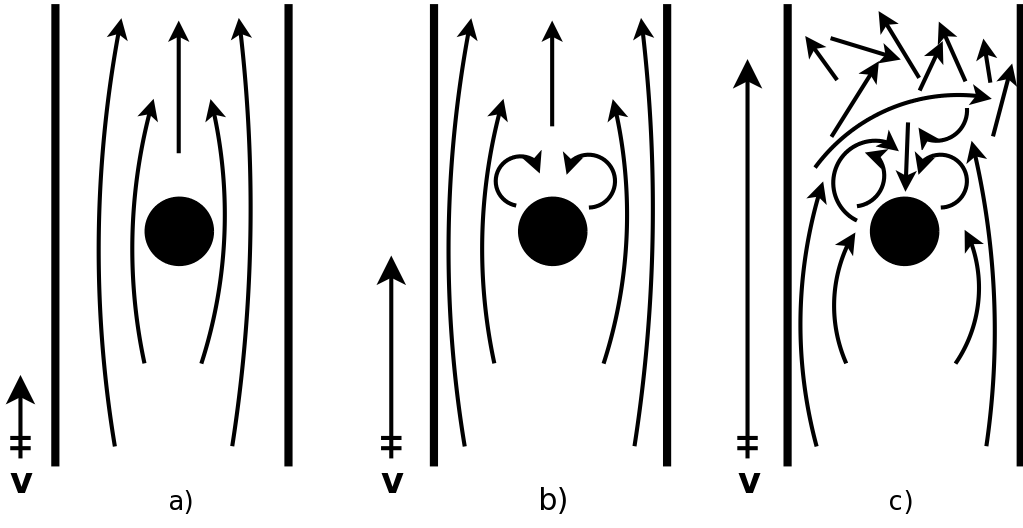
An dieser Stelle wird an einem kurzen Beispiel die Chaostheorie verdeutlicht. Das Beispiel geht zurück auf Haken (Hak91, S. 59), wurde aber für diese Arbeit abgewandelt. Man stelle sich einen idealen geradlinigen Wasserkanal vor, wie in Abbildung 4 auf Seite gezeigt. In dessen Mitte befindet sich ein Zylinder, um den das Wasser herumströmt. Bei niedriger Fließgeschwindigkeit wird keine Auffälligkeit zu beobachten sein (Abbildung 4 Teilbild a)). Das Wasser strömt gleichmäßig um den Zylinder. Erhöht man die Fließgeschwindigkeit kontinuierlich, werden sich ab einer bestimmten Geschwindigkeit Wirbel im Wasser hinter dem Zylinder bilden, wie in Abbildung 4 Teilbild b) gezeigt. Die Wirbelbildung ist ein Attraktor. Das Umschlagen des Verhaltens des fließenden Wassers stellt eine Bifurkation dar. Durch eine weitere Erhöhung der Fließgeschwindigkeit nehmen die Wirbel zu und das Verhalten des Wassers hinter dem Zylinder wird dadurch zunehmend komplizierter zu beschreiben. Bei der weiteren Erhöhung der Fließgeschwindigkeit wird ein weiterer Bifurkationspunkt erreicht. Danach bewegt sich das Wasser hinter dem Zylinder völlig chaotisch (Abbildung 4 Teilbild c)) und es lässt sich kein klares Verhalten, wie z. B. Wirbel, erkennen. Somit streben die Trajektorien, die den Zustand des Wassers hinter dem Zylinder beschreiben, auf den seltsamen Attraktor zu.

Abbildung: Chaostheorie am Beispiel Wasserströmung in Kanal

In diesem Gedankenexperiment wurde lediglich die Fließgeschwindigkeit des Wassers erhöht. Trotzdem ergab sich daraus völlig unerwartetes (nicht-deterministisches) und spontanes (nicht-lineares) Verhalten. Dies entspricht dem Gedanken der Emergenz.